Тестовые данные в машинном обучении

Что такое тестовые данные?

Тестовые данные в машинном обучении представляют собой часть набора данных, используемую для оценки качества и производительности модели. В отличие от обучающих данных, которые помогают модели выявлять закономерности и разрабатывать алгоритмы принятия решений, тестовые данные предназначены для финальной проверки того, как модель работает с информацией, с которой она ранее не сталкивалась. 

Использование тестового набора данных

• Финальная оценка: Независимая оценка качества модели после завершения обучения и настройки.
• Проверка обобщения: Оценка способности модели справляться с ранее не встречавшимися данными.
• Анализ ошибок: Выявление систематических ошибок и слабых мест модели.
• Сравнение моделей: Использование одного тестового набора для сопоставления разных моделей или их версий.

Как связаны тестовые, валидационные и обучающие данные?

При разработке модели машинного обучения исходный набор данных разделяют на три части: обучающую, валидационную и тестовую выборки. Такое разделение необходимо для корректного построения модели и объективной оценки ее работы.

• Обучающий набор (Training Set): Основная часть данных, которая используется для обучения модели.
• Валидационный набор (Validation Set): Необходим для тонкой настройки гиперпараметров и оптимизации производительности модели во время обучения. 
• Тестовый набор (Test Set): Применяется для окончательной оценки модели. Он позволяет проверить, насколько хорошо алгоритм справляется с новыми данными и готов ли он к использованию в реальных условиях.

Важно: тестовые данные должны оставаться полностью независимыми от обучающего и валидационного наборов, чтобы избежать утечки данных (data leakage).

Методы разделения данных

Корректное разделение данных на обучающий, валидационный и тестовый наборы во многом определяет успешность модели в реальной среде. Существует несколько подходов к тому, как именно разделять данные, включая простое случайное разделение, стратифицированный отбор и методы перекрестной проверки (K‑Fold Cross-Validation).

Методы обеспечения качества и актуальности данных

Подготовка тестовых данных является важным этапом в разработке моделей машинного обучения. Хорошо подготовленные данные обеспечивают объективную оценку функциональности модели, ее способности к обобщению и устойчивости к ошибкам и непредвиденным ситуациям.

Очистка данных

Очистка данных направлена на устранение ошибок, дубликатов и некорректных значений, которые могут негативно повлиять на качество модели. Важной частью этого процесса является обработка пропущенных данных, которая может включать их удаление или заполнение наиболее вероятными значениями, например, средним, медианой или модой соответствующего признака.

Валидация данных 

Для успешного тестирования модели необходимо убедиться, что данные соответствуют установленным стандартам и требованиям, включая допустимые диапазоны значений, единообразие форматов и корректность информации. Важным этапом подготовки является нормализация числовых признаков, приводящая их к единой шкале (например, от 0 до 1 или от ‑1 до 1). Это позволяет избежать ситуации, когда один признак оказывает непропорционально сильное влияние на модель по сравнению с другими из-за различий в масштабах (если один признак имеет диапазон от 0 до 1000, а другой — от 0 до 1).

Согласование тестовых данных с обучающими данными

Тестовые данные должны соответствовать формату обучающего набора. Если структура данных отличается, это может привести к ошибкам в предсказаниях и некорректной интерпретации результатов.

Обновление данных

Важно следить за тем, чтобы тестовый набор данных оставался репрезентативным для задач, где данные со временем меняются. Если модель используется в динамически меняющейся среде, например в системах рекомендаций или прогнозирования спроса, обновление данных может включать не только добавление новых примеров, но и удаление устаревших записей, чтобы оценка модели была актуальной и отражала реальные условия.

Характеристики высококачественных тестовых данных

Использование высококачественных тестовых данных имеет решающее значение для разработки моделей машинного обучения, поскольку это влияет на точность и эффективность процесса тестирования. Ниже приведены ключевые характеристики высококачественных тестовых данных:

Метрики оценки качества

Метрики классификации

При оценке качества модели машинного обучения важно использовать метрики, которые объективно отражают ее предсказательную способность. Разные метрики позволяют анализировать различные аспекты работы модели, особенно в задачах классификации, где важно учитывать не только общее количество верных предсказаний, но и характер ошибок.

Перед рассмотрением ключевых метрик классификации разберемся с основными понятиями, используемыми в матрице ошибок (confusion matrix):

• TP (True Positive) — модель правильно предсказала положительный класс.
• FP (False Positive) — модель ошибочно предсказала положительный класс, хотя реальный класс отрицательный.
• TN (True Negative) — модель правильно предсказала отрицательный класс.
• FN (False Negative) — модель ошибочно предсказала отрицательный класс, хотя реальный класс положительный.

Используя эти категории, можно рассчитать ключевые метрики классификации:

Accuracy (Общая точность)

Доля правильных предсказаний из общего числа предсказаний. Рассчитывается как отношение суммы истинно положительных (TP) и истинно отрицательных (TN) примеров ко всем предсказаниям:

$$ Accuracy = \frac{TP + TN}{TP + TN + FP + FN} $$

Несмотря на простоту и наглядность, этот показатель может быть обманчивым, если набор данных сильно несбалансирован (когда один из классов встречается гораздо чаще других).

Precision (Точность)

Определяет, какая доля объектов, предсказанных моделью как положительные, действительно относится к положительному классу. Рассчитывается по формуле:

$$ Precision = \frac{TP}{TP + FP} $$

Высокая точность означает, что модель редко ошибочно относит объекты к положительному классу. Эта метрика особенно важна в задачах, где критичны ложные срабатывания (FP), например, при диагностике заболеваний или обнаружении мошеннических транзакций.

Recall (Полнота)

Показывает, какую часть объектов, принадлежащих к положительному классу, модель классифицировала правильно. Эта метрика вычисляется следующим образом:

$$ Recall = \frac{TP}{TP + FN} $$

Чем выше полнота, тем меньше случаев, когда модель пропускает положительные примеры. Это критично в задачах, где важно минимизировать ложные отрицательные предсказания.

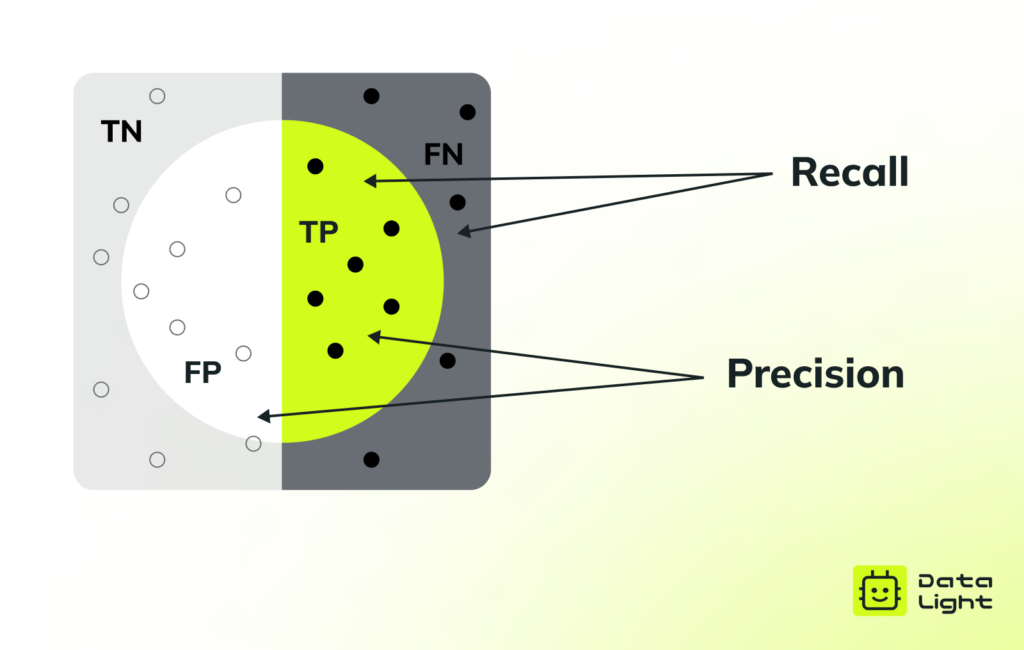
Основное различие между Precision и Recall

• Precision фокусируется на качестве положительных предсказаний: если модель предсказала объект как положительный, насколько часто это оказалось верным?
• Recall фокусируется на количестве найденных положительных объектов: из всех существующих положительных примеров сколько модель действительно обнаружила?

Пример: обнаружение спама

Представьте, что мы создаем модель для фильтрации спам-писем:

• Высокая Precision, но низкая Recall → Фильтр очень осторожен: он помечает как спам только те письма, в которых он абсолютно уверен (например, содержащие много подозрительных слов). В результате почти все письма, отмеченные как спам, действительно являются спамом, но при этом модель пропускает мимо много настоящего спама.
• Высокая Recall, но низкая Precision → Фильтр старается найти весь возможный спам и начинает помечать слишком много писем как спам. В результате модель замечает почти весь спам, но ошибочно отправляет в спам-папку и некоторые обычные письма.

Чтобы уравновесить Precision и Recall, используется F1-метрика.

F1-метрика

Представляет собой гармоническое среднее между точностью и полнотой:

$$ F1 = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall} $$

F1-метрика используется, когда важно найти баланс между точностью и полнотой, особенно в случаях несбалансированных классов. Высокий показатель означает, что модель хорошо справляется с классификацией, не жертвуя точностью ради полноты или наоборот.

Метрики регрессии

Для задач регрессии, где модель предсказывает непрерывные значения (например, цену недвижимости или температуру), используются специальные метрики, оценивающие степень отклонения предсказанных значений от реальных.

Mean Squared Error (MSE) — Среднеквадратичная ошибка

MSE рассчитывает среднее значение квадратов разницы между предсказанными и реальными значениями:

$$ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i — \hat{y}_i)^2 $$

Здесь: ​ — предсказанное значение, — истинное значение.

где: $\hat{y}_i$ — предсказанное значение, $y_i$ — истинное значение.

Эта метрика сильно штрафует большие ошибки, так как разница возводится в квадрат. MSE особенно чувствительна к выбросам, поэтому ее используют, когда важно выявлять крупные отклонения.

Root Mean Squared Error (RMSE) — Корень из среднеквадратичной ошибки

RMSE — это квадратный корень из MSE:

$$ RMSE = \sqrt{MSE} $$

В отличие от MSE, RMSE имеет ту же размерность, что и целевой признак, что делает интерпретацию ошибки более удобной. Он также чувствителен к выбросам, но дает представление о среднем уровне ошибки в тех же единицах измерения, что и предсказываемые значения.

Mean Absolute Error (MAE) — Средняя абсолютная ошибка

MAE измеряет среднее абсолютное отклонение предсказанных значений от реальных:

$$ MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i — \hat{y}_i| $$

В отличие от RMSE, MAE учитывает все ошибки одинаково, что делает ее менее чувствительной к выбросам.

Основное различие между RMSE и MAE

• RMSE сильнее наказывает большие ошибки из-за квадратичного характера формулы, поэтому подходит для случаев, где критично минимизировать крупные отклонения.
• MAE дает более равномерную оценку всех ошибок и лучше работает, когда выбросы встречаются редко или их влияние не так важно.

Выбор метрики зависит от задачи: если важно не пропускать большие ошибки, лучше использовать RMSE; если нужна более устойчивая к выбросам оценка, предпочтительнее MAE.

Какой объем тренировочных данных необходим?

Определить оптимальный объем тренировочных данных — все равно что собрать вещи в дорогу: слишком мало — и вы не готовы; слишком много — и вы перегружены. Идеальное количество зависит от нескольких факторов:

• Сложность модели: Для эффективной работы простых моделей (например, линейной регрессии) требуется меньше данных по сравнению со сложными моделями, такими как глубокие нейронные сети.
• Сложность задачи: Для более сложных задач требуется больше примеров данных.
• Качество данных: Если данные содержат мало шума, дублирующихся или нерелевантных примеров, модель может обучаться быстрее и эффективнее, требуя меньшего количества примеров.
• Эмпирическое тестирование: Используйте такие методы, как кривые обучения, чтобы оценить, как меняется производительность модели с увеличением объема данных.

Проблемы при обучении и оценке качества модели

Обучение и оценка моделей машинного обучения сопряжены с рядом проблем, которые могут повлиять на их производительность и надежность. Ниже приведены некоторые распространенные проблемы и возможные решения для улучшения качества модели.

Переобучение и недообучение

• Переобучение (overfitting) возникает, когда модель слишком точно подстраивается под обучающие данные, запоминая не только полезные закономерности, но и случайный шум. В результате она демонстрирует высокую точность на тренировочных примерах, но плохо справляется с новыми, ранее не встречавшимися данными. 

Такое поведение говорит о том, что модель обладает низкой обобщающей способностью. Переобучение часто наблюдается в сложных моделях с большим числом параметров, особенно если обучающая выборка невелика или содержит избыточную информацию.

• Недообучение (underfitting) происходит, когда модель недостаточно сложна для выявления закономерностей в данных. Она не способна эффективно извлекать ключевые признаки, что приводит к низкой точности как на обучающем, так и на тестовом наборе. 

Недообучение часто связано с выбором слишком простой модели, недостатком данных или неправильными гиперпараметрами, ограничивающими ее обучаемость.

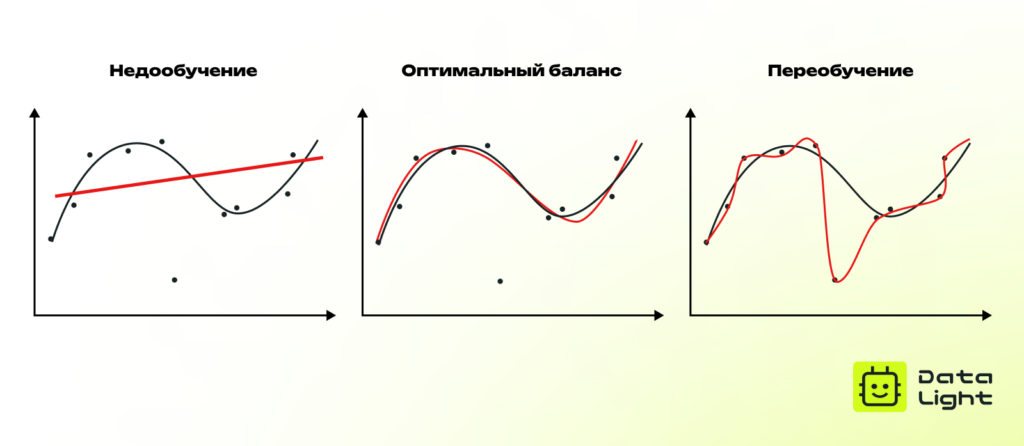
Обе проблемы снижают практическую ценность модели: переобученная модель ведет себя непредсказуемо на реальных данных, а недообученная — не может решать поставленную задачу. Оптимальный баланс достигается за счет тщательной настройки гиперпараметров, подбора достаточного количества данных и применения методов регуляризации.

Предвзятость или недостаточность тестовых данных

Тестовые данные играют ключевую роль в объективной оценке качества модели. Если они не отражают реальное распределение данных, это может привести к искаженным результатам и ненадежным прогнозам.

• Предвзятость тестовых данных возникает, когда тестовая выборка отличается от данных, с которыми модель будет работать в реальных условиях. 
• Недостаточность тестовых данных означает, что выборка слишком мала для корректной оценки производительности модели. 

Проблемы предвзятости и недостаточности сопряжены с тем, что модель может показывать хорошие результаты в рамках тестирования, но работать нестабильно на новых данных.

Решения:

1. Стратифицированная выборка помогает сделать тестовый набор более сбалансированным: весь набор данных делится на несколько подгрупп (страт) в соответствии с ключевыми характеристиками, и затем из каждой страты пропорционально выбирается подвыборка. Это позволяет учитывать редкие классы и избегать смещения в сторону преобладающих категорий.
2. Дополнительно можно использовать генерацию синтетических данных или бутстрэппинг (bootstrap resampling) — техники, позволяющие искусственно расширять тестовую выборку.

Ключевые выводы

Тестовые данные играют важнейшую роль в оценке и улучшении моделей машинного обучения. Хорошо подготовленный тестовый набор данных обеспечивает объективную оценку производительности модели в реальных условиях, помогая тонко настроить модель и улучшить ее способность к обобщению.